I've written three esoteric programming languages, titled L3, Dungeon Journey, and Archipelago, along with code-golf challenges for the languages. The languages were used in the 2023, 2024, and 2025 Carnegie Mellon Informatics and Mathematics Competition’s programming contest. You may find the original language specifications and problems on the CMIMC website. These esolangs have been designed with three goals in mind 1. Coupling of data access and control flow 2. Native support for sequences of data. 3. Interesting visual appeal.
L3 consists of program code that manipulates a variable of 10 registers, with operations roughly corresponding to that of a Minsky machine. The program code and control flow is laid out on a 2D grid. L3X is much more interesting. It extends L3 by allowing multiple pieces of data to flow around the program simultaneously. Much of the interest for coding in L3/L3X is the routing aspect, placing the program on the grid efficiently and perhaps elegantly. You can check out a slightly newer handout, the web-based visualizer and some example code.
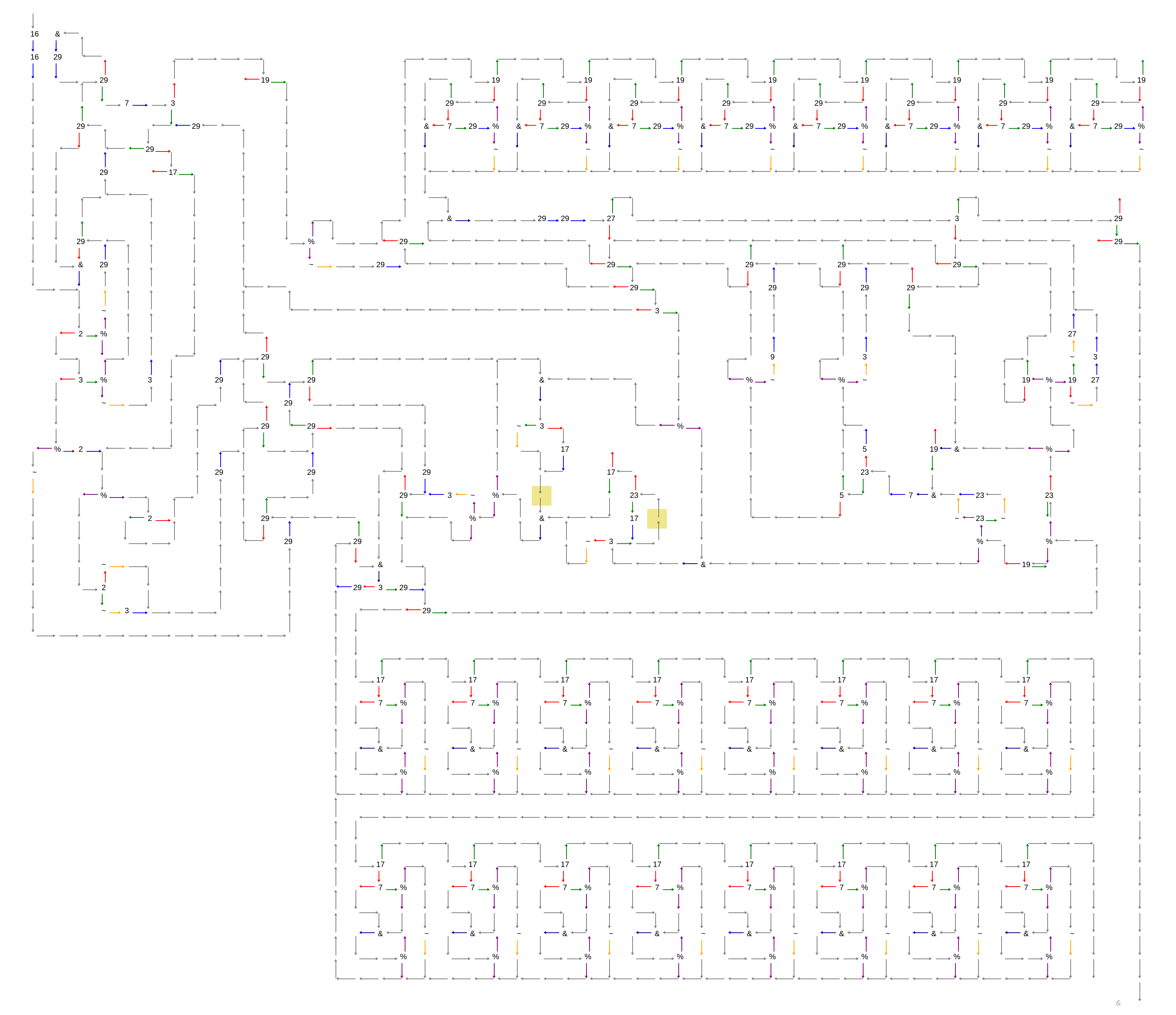
Shown below is an interpreter for an ordinary 8-registry Minsky machine holding up to 16 instructions. The memory size can be easily expanded. You can find the code along with a simple Fibonacci number program that runs on the Minsky machine in the examples.

Dungeon Journey is best described as a Turing machine with a 2D tape, two tape heads, and no internal state. The two tape head part somewhat resemble real computers, which maintain at least an instruction pointer and a stack pointer. The 2D tape part resembles Langton's ant and Turmites. Indeed, Dungeon Journey can also exhibit similar chaotic behavior on an empty tape, though chaotic behavior is generally much harder to encounter due to the lack of internal state (the direction) that allows for more mixing. On the flip side, with two tape heads one can intentionally draw shapes much easier.
Shown in figure 3 are various patterns drawn in Dungeon Journey, from orderly to chaotic. Shown in figure 4 is one of the most interesting Dungeon Journey program I have seen, as it alternates between a regular double pyramid pattern and chaos after collisions.


Archipelago code involves an instruction pointer walking along the boundary of islands separated by the ocean, represented as connected components of regions on a 2D grid. Instructions are placed on the boundary tiles on the island. Each island contains its own stack, and instructions allow an island to communicate with another island within its line of sight. Although Turing-completeness is likely achievable with only two islands, like how L3X is Turing-complete with just L3, it is more interesting to consider sequences of data passed along multiple islands. The difficulty of Archipelago comes from the placement of islands due to the walk along boundary and line of sight limitations. You can check out the web-based visualizer and some example code.

Within a group of four, we made the OpenGL-based game Swordmaster for the course CMU 15-466 computer game programming. The game uses collision physics for sword collisions. The sword animations, scene and sound effects are all handmade. See its itch.io page.

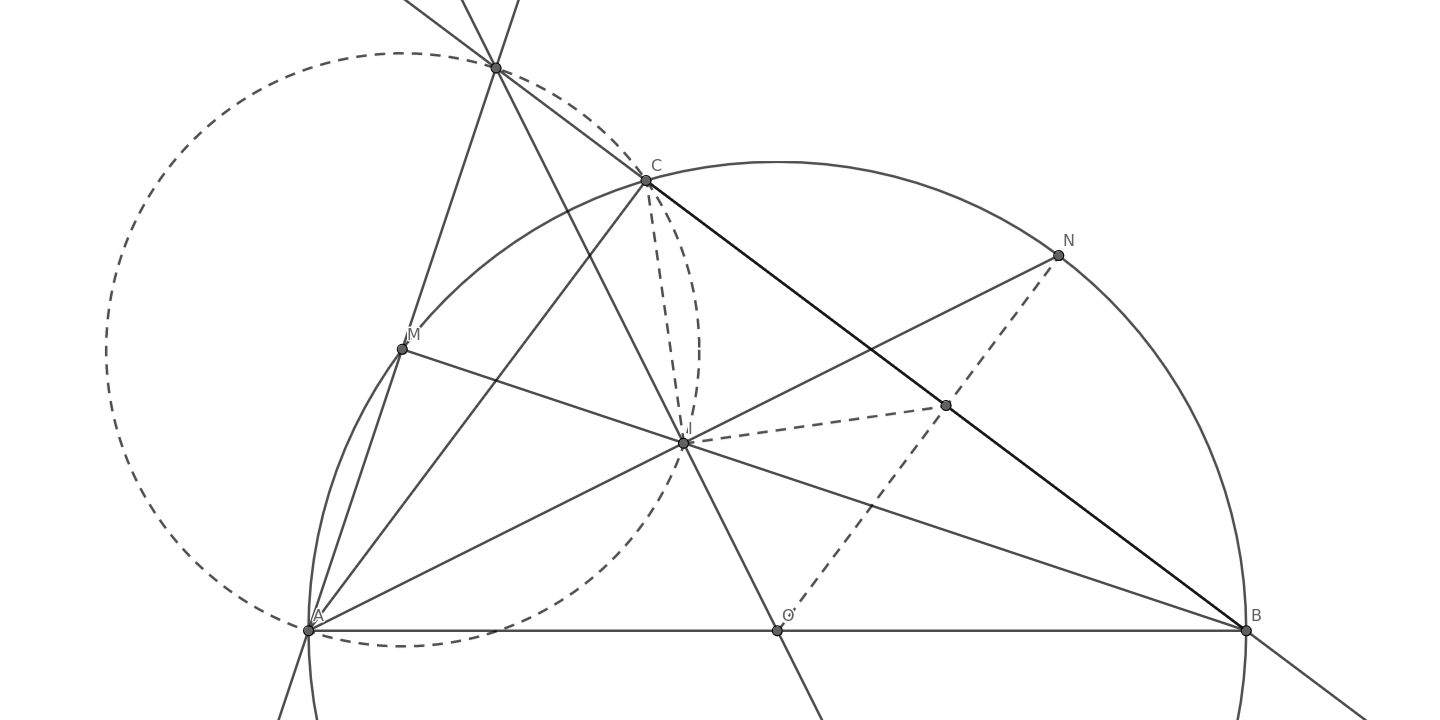
I've written a handout on synthetic geometry with a philosophy that focuses on underlying ideas and constructions instead of theorems, and I included many hand-picked problems grouped by common ideas. The handout totals to nearly 120 pages, and was first released in January 2022. Here is the main handout, solution to examples, and solution to problems.